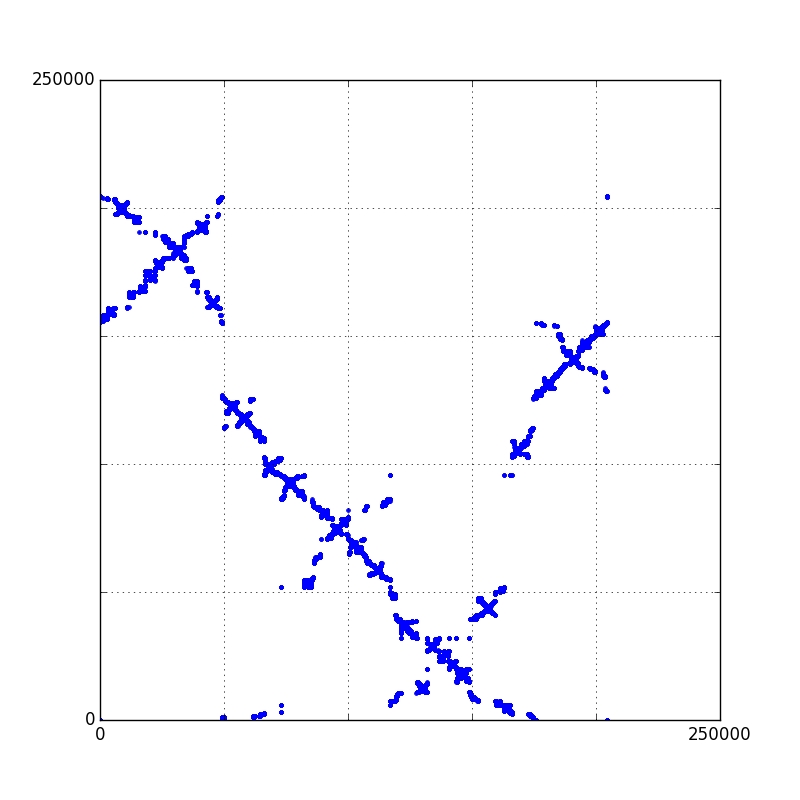
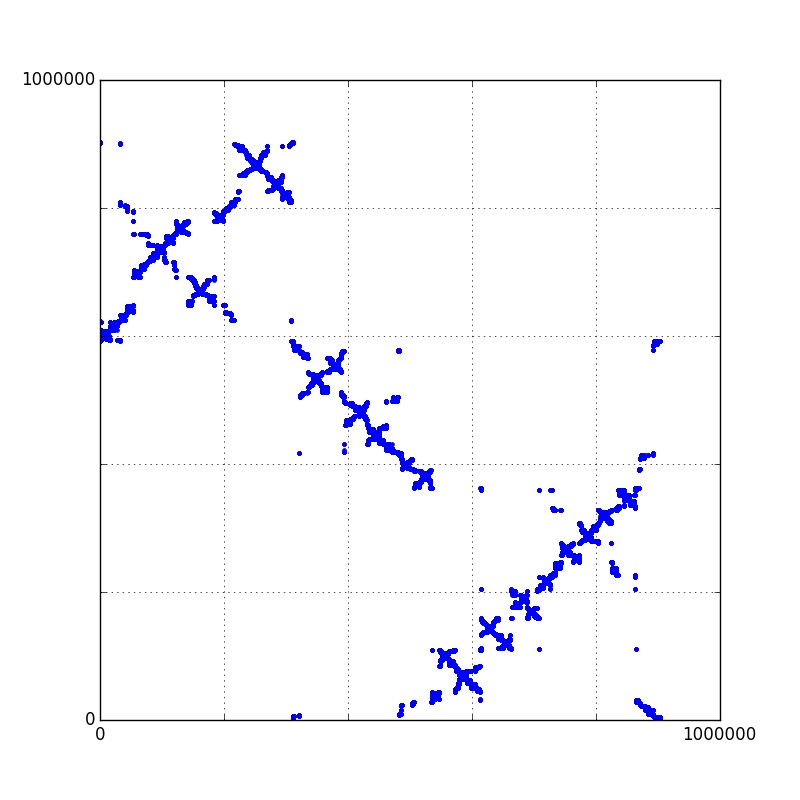
This represents the diagrams of two large separable permutations, taken uniformly at random: for each \(i\), there is a dot at coordinates \( (i,\sigma(i))\). It converges towards a Brownian limiting object, that we called Brownian separable permuton. The same limit arises for uniform random permutations in a large family of permutation classes. See details in the following articles:

• The Brownian limit of separable permutations, with Frédérique Bassino, Mathilde Bouvel, Lucas Gerin and Adeline Pierrot.
  Annals of Probability, 46 (4), pp. 2134-2189, 2018, arXiv.
  
• Universal limits of substitution-closed permutation classes, with Frédérique Bassino, Mathilde Bouvel, Lucas Gerin, Mickaël Maazoun and Adeline Pierrot.
  Journal of European Mathematical Society, 22 (11), pp. 3565–3639, 2020, arXiv.
• A decorated tree approach to random permutations in substitution-closed classes, with Jacopo Borga, Mathilde Bouvel, and Benedikt Stufler.
  Electronic Journal of Probability, 25, paper no. 67, pp. 1-52, 2020, arXiv.
• Scaling limits of permutation classes with a finite specification: a dichotomy, with Frédérique Bassino, Mathilde Bouvel, Lucas Gerin, Mickaël Maazoun and Adeline Pierrot.
  Advances in Mathematics, vol. 405, Article 108513, 2022, arXiv.